A Brief Overview of Causal Inference

class: center, middle, inverse, title-slide

# A Brief Overview of Causal Inference
### Todd R. Johnson, PhD <br> Professor<br><br>
### The University of Texas School of Biomedical Informatics at Houston
### 2020-01-29<br><span class="footnote">Use arrow keys to navigate, press h for help</span>

---

# Notes

Use the arrow keys to navigate. Press `h` for help. Press `p` to see speaker notes. These notes often elaborate on slide content and include additional material and references.

My primary objective for creating this is to help me understand the basics of causal infererence. I hope to use it to help others as well, especially machine learning researchers who tend to make predictive associative models, rather than causal models.

This presentation is hosted on Github Pages at: https://tjohnson250.github.io/overview_causal_infererence/overview_causal_infererence.html#1

All of these slides, including model outcomes, are generated in R using R Markdown and the [xaringan](https://github.com/yihui/xaringan) presentation package. The source code to generate the presentation is at: https://github.com/tjohnson250/overview_causal_infererence

A shorter version, suitable for a one hour seminar, may be checked out from the `short` branch: https://github.com/tjohnson250/overview_causal_inference/tree/short

If you find errors or have suggestions for improvement, open an issue on this project's Github repo.

---
# Pearl's Three Layer Causal Hierarchy.fn[1]

<table class="table" style="width: auto !important; margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> Level </th>
   <th style="text-align:left;"> Typical.Activity </th>
   <th style="text-align:left;"> Typical.Questions </th>
   <th style="text-align:left;"> Example </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;font-weight: bold;color: #1c5253 !important;"> 1. Association<br>$\mathbf{P(y|x)}$ </td>
   <td style="text-align:left;width: 8em; "> Seeing,<br>Observing </td>
   <td style="text-align:left;width: 8em; "> How would seeing X change my belief in Y? </td>
   <td style="text-align:left;"> What is my chance of having prostate cancer if my PSA test is 3 ng/ml? </td>
  </tr>
  <tr>
   <td style="text-align:left;font-weight: bold;color: #1c5253 !important;"> 2. Intervention<br>$\mathbf{P(y|do(x), z)}$ </td>
   <td style="text-align:left;width: 8em; "> Doing,<br>Intervening </td>
   <td style="text-align:left;width: 8em; "> What if I do X? </td>
   <td style="text-align:left;"> Will taking aspirin daily reduce my risk of stroke? </td>
  </tr>
  <tr>
   <td style="text-align:left;font-weight: bold;color: #1c5253 !important;"> 3. Counterfactuals<br>$\mathbf{P(y_x|x',y')}$ </td>
   <td style="text-align:left;width: 8em; "> Imagining,<br>Retrospecting </td>
   <td style="text-align:left;width: 8em; "> Was it X that caused Y?<br>What if I had acted differently? </td>
   <td style="text-align:left;"> If I had stopped smoking 10 years earlier, could I have prevented lung cancer? </td>
  </tr>
</tbody>
</table>

.footnote[[1] Pearl, 2019]

???
I have modified this with what I think are more illustrative questions. This is based on the paper below, but also appears in other publications by Pearl.

Pearl J. The seven tools of causal inference, with reflections on machine learning. Communications of the ACM. 2019 Feb 21;62(3):54-60.

---
class: middle

### Part I: Causation

### Part II: Identifying and Estimating Causal Effects from Observational Data

### Part III: Causal Model Evaluation

### Part IV: Causal Discovery from Observational Data

### Part V: Counterfactual Reasoning

---
class: center, middle

# Part I: Causation

---
# Part I Learning Objectives: Causation
- Define and identify interventions, causal effects, and average causal effects
- Given a generative model, draw the corresponding causal DAG
- Given a causal DAG describe the DAG that would result from an intervention on one of the variables
- Given data on two interventions, calculate the average causal effect

---
# Example: Age, Exercise and Cholesterol
Suppose that the following model accurately describes how age, exercise, and cholesterol are related

.pull-left[

.pull-right[
From the model, the causal effect of exercise on cholesterol is `$-1e$`:

- For every unit increase in excercise, cholesterol decreases by `$1$`
  
Causal DAG (Directed Acyclic Graph)
  - Graphical representation of the data generating model
  - Links represent *possible* direct causal effects
  - Missing links indicate the strong assumption of no direct causal effect
  - Must include all common causes of any pair of variables already in the DAG
]

---
## The Observational Model Produces Observational Data
<div id="htmlwidget-c73aca6c7ad84950d112" style="width:100%;height:auto;" class="datatables html-widget"></div>
<script type="application/json" data-for="htmlwidget-c73aca6c7ad84950d112">{"x":{"filter":"none","fillContainer":false,"data":[["1","2","3","4","5","6","7","8"],[11.45765568885,13.735252382825,10.8003906141084,11.5365219829436,17.4411290088925,15.915540805092,12.795310382867,12.4610897267829],[40.4544507199996,46.4023827884939,33.4554367853455,37.8232211168603,56.3651467693854,56.3921684606149,42.1552770897148,36.3918492270746],[112.264682573506,113.361571285911,111.605070068514,110.754175619267,118.994453921155,114.692655209124,104.214292725906,107.01192532354]],"container":"<table class=\"nowrap hover\">\n  <thead>\n    <tr>\n      <th> <\/th>\n      <th>E<\/th>\n      <th>A<\/th>\n      <th>C<\/th>\n    <\/tr>\n  <\/thead>\n<\/table>","options":{"pageLength":8,"dom":"t","columnDefs":[{"className":"dt-right","targets":[1,2,3]},{"orderable":false,"targets":0}],"order":[],"autoWidth":false,"orderClasses":false,"lengthMenu":[8,10,25,50,100],"rowCallback":"function(row, data) {\nDTWidget.formatRound(this, row, data, 1, 2, 3, ',', '.');\nDTWidget.formatRound(this, row, data, 2, 2, 3, ',', '.');\nDTWidget.formatRound(this, row, data, 3, 2, 3, ',', '.');\n}"}},"evals":["options.rowCallback"],"jsHooks":[]}</script>
---
.pull-left[
### The observational data show that exercise increases cholesterol!
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-4-1.png" width="70%" />

`$c = 102.42+0.5e \space (p<.001)$`
]

.pull-right[
### But in the model that generated the data exercise decreases cholesterol!

```r
n <- 10000
a <- rnorm(n, mean = 50, sd = 10)
e <- 0.3*a + rnorm(n)
*c <- 0.5*a + -1*e + rnorm(n, mean = 100, sd = 5)
```
![](overview_causal_inference_files/figure-html/unnamed-chunk-6-1.png)
Why does the data show the opposite association?
]

---

# Definitions

- **Causal Infererence** is the process of inferring the **causal effect** of one random variable, `$X$`, on a second random variable. `$Y$`
- The **Causal Effect** of `$X$` on `$Y$` is the expected value of `$Y$` when we **intervene** to directly set the value of `$X$`
- **Intervening** on `$X$` means to force `$X$` to take a specific value, independent of any of the variables that normally influence the value of `$X$`
    - Suppose that the decision to treat is normally influenced only by gender, *intervening* means ignoring gender when deciding on treatment, such as by randomly assigning whether to treat or not  
- This is why Randomized Controlled Trials (RCT's) are considered the gold standard for identifying causal effects

---
## Intervening Changes the Generative Model
Intervene by randomly setting `$E$` from `$0 - 20$`
.pull-left[
### Observational Model

```r
n <- 10000
a <- rnorm(n, mean = 50, sd = 10)
*e <- 0.3*a + rnorm(n)
c <- 0.5*a + -1*e + rnorm(n, mean = 100, sd = 5)
```
![](overview_causal_inference_files/figure-html/unnamed-chunk-8-1.png)
]

.pull-right[
### Interventional Model

```r
n <- 10000
a <- rnorm(n, mean = 50, sd = 10)
*e <- sample(0:20, n, replace = TRUE)
c <- 0.5*a + -1*e + rnorm(n, mean = 100, sd = 5)
```
![](overview_causal_inference_files/figure-html/unnamed-chunk-9-1.png)
]
???
Intervening on `$E$`, means replacing the expression for `$e$` from the observational model with a specific value, here one randomly assigned between `$0$` and `$20$`. This changes the generative model and also changes the causal DAG by removing the link `$A \rightarrow E$`, since in the intervential model, `$e$`'s value no longer directly depends on `$a$`.

---
## Intervening Changes The Distribution

.pull-left[
### Observational Distribution
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-10-1.png" width="70%" />

`$c = 102.42+0.5e \space (p<.001)$`
]

.pull-right[
### Interventional Distribution
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-11-1.png" width="70%" />

`$c = 125.19+-1.02e \space (p<.001)$`
]

???
The coefficient for `$e$` on the observational distribution is way off (indicating that exercising increases cholesterol), but the coefficient for the interventional distribution is close to the true value. Both coefficents are statistically significant at the p = .001 level.

---
# Difference Between Seeing and Doing
.pull-left[
### Observational Association
`$E(C|e)$`: The expected value of Cholesterol given that we observe a specific level of exercise.

`$E(C|e)$` is confounded, because age `$A$` affects both the amount of exercise `$E$` a person gets and cholesterol levels `$C$`.

In the observational data
`$$E(C|e) \neq E(C|do(e))$$`
]
.pull-right[
### Interventional Association (Causal Effect)
`$E(C|do(e))$`: The expected value of Cholesterol given that we intervene and set exercise to a specific value, independent of any of the variables that normally influence the value of `$E$`.

`$do()$` is called the do-operator.

In the interventional data
`$$E(C|e) = E(C|do(e))$$`
]

---
### Average Causal Effect (ACE) for a Population
Contrast of the mean values of `$Y$` (outcome) given two specific interventions on `$X$` (treatment)

- Dichotomous (binary) treatment and outcomes:

`$$P(Y=1|do(X = 1)-P(Y=1|do(X = 0)))$$`
    
    `$$P(Survival|do(Treat))-P(Survival|do(Don't Treat))$$`

- Continuous treatment and outcomes:

`$$E(Y|do(X=x)) - E(Y|do(X=x^{\prime})$$`

First equation is a special case, since for dichotomous outcomes 
  `$$E(Y|do(X=x)) = P(Y=1|do(X = x))$$`
???
ACE is also called the Average Treatment Effect (ATE)

Contrast ACE with the individual causal effect: the difference between counterfactual outcomes for a single patient--the outcome if treated vs. the outcome if not treated. Lack of an average causal effect does not imply lack of an individual causal effect. However, in most cases it is impossible to estimate individual causal effects from observational data because we only ever observe the effect of one level of the treatment for an individual.

A crossover randomized experiment in which we give different treatments over time to the same person can sometimes measure individual causal effects when treatment and outcome are short term and do not affect the next treatment period. This is commonly used in cognitive science  and psychology in within-subject designs. For example, we might measure a subject's ability to monitor different numbers of patients using a telemonitoring system to determine the effect of patient load on time to respond to events, error rate, etc.

See Hernan and Robbins, Causal Inference, Chapter 1 and Fine Point 2.1 for more details in individual vs. population causal effects. https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/

---
## Estimating ACE of Exercise on Cholesterol Using the Interventional Dataset
Step 1: Estimate functional relationship between C and E using linear regression on the **interventional dataset**:

`$$c = 125.19+-1.02e \space (p<.001)$$`

`$$E(C|do(E=e))=125.19+-1.02e \space (p<.001)$$`

Step 2: Use regression equation to calculate ACE

$$
`\begin{align}
  ACE &= E(Y|do(E=1))-E(Y|do(E=2)) \\
      &= (125.19+-1.02*1) - (125.19+-1.02*2) \\
      &= 123.16 - 124.17 \\
      &= -1.02
\end{align}`
$$
Equivalently: The regression coefficent on `$e$` directly tells us how much `$C$` will change for each unit increase in `$E$`.

---
class: center, middle, Large

We say that `$\mathbf{X}$` **causes** `$\mathbf{Y}$` in a population when the **average causal effect** of `$X$` on `$Y$` is non-zero.

---
class: center, middle

## Part II: Identifying and Estimating Causal Effects from
## Observational Data

---
# Part 2 Learning Objectives: Identifying and Estimating Causal Effects from
## Observational Data

- Distinguish between total and direct causal effects with respect to a Causal DAG
- Define adjustment and show how to adjust for a variable when doing linear regression
- Given a causal DAG identify the causal and non-causal paths between two variables
- Apply the backdoor criterion to identify which variables must be adjusted for in order to identify direct and total causal effects
- Write a regression expression to estimate the causal effect of `$X$` on `$Y$` given a set of variables that meet the backdoor criterion
- Given the results of a linear regression that satisfies the backdoor criterion for the causal effect of `$X$` on `$Y$` give the causal effect estimate of `$X$` on `$Y$`

---
## With Observational Data...
.pull-left[
#### using E to predict C gives an incorrect estimate,
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-13-1.png" width="70%" />

`$c = 102.42+0.5e \space (p<.001)$`
]

.pull-right[
#### but controlling for A gives the correct estimate
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-14-1.png" width="70%" />

`$c = 99.99+-0.93e + 0.48a \space (p<.001)$`
]
???
The graph on the right shows the observational data with a regression line for each of several age groups. As you can see, most of the lines show the appropriate negative correlation between `$C$` and `$E$`. Lines near the left and right are incorrect due to sparse data. Stratifying by age (here age group) is one method for controlling or adjusting for a confounder, such as `$A$`.

The regression equation also shows a very close estimate of the correct causal effect of `$E$` on `$C$`. Regressing `$C$` on both `$E$` and `$A$` controls or adjusts for `$A$`, returning the close estimate of the true causal effect of `$E$` on `$C$`.

---
## Adjustment
Stratifying by age `$(A)$` or including `$A$` as a covariate in the regression `$(C = {\beta_1}+{\beta_2}A + {\beta_3}E)$` is called **adjusting**, **conditioning**, or **controlling for A**

In R code, regression using the observational dataset (`dobs`):
.pull-left[
Unadjusted for `$A$`

```r
lm(C ~ E, dobs)
```

```
## 
## Call:
## lm(formula = C ~ E, data = dobs)
## 
## Coefficients:
## (Intercept)            E  
##    102.4250       0.5043
```
]
.pull-right[
Adjusted for `$A$`

```r
lm(C ~ E + A, dobs)
```

```
## 
## Call:
## lm(formula = C ~ E + A, data = dobs)
## 
## Coefficients:
## (Intercept)            E            A  
##      99.991       -0.931        0.479
```
]
---
### What is the Causal Effect of Age on Cholesterol?
Using the observational dataset, regressing `$C$` on `$A$` and `$E$` gave us: `$c = 99.99+-0.93e + 0.48a$`
.pull-left[

```r
n <- 10000
a <- rnorm(n, mean = 50, sd = 10)
e <- 0.3*a + rnorm(n)
*c <- 0.5*a + -1*e + rnorm(n, mean = 100, sd = 5)
```
![](overview_causal_inference_files/figure-html/unnamed-chunk-18-1.png)
]
.pull-right[
From the model, the **direct causal effect** of `$A$` on `$C$` is `$0.5a$`

- Regressing `$C$` on `$A$` and `$E$` closely estimates this effect.

- However `$A$` also affects `$C$` through `$E$`

The **total causal effect** of `$A$` on `$C$` includes the effect of `$A$` through both paths,  which from the model is:

$$
`\begin{align}
  c &= .5a + -1\mathbf{e} \\
    &= 0.5a + -1\mathbf{(0.3a)} \\
      &= 0.5a\mathbf{- 0.3a} \\
      &= 0.2a \\
\end{align}`
$$

]

???
To get the total causal effect of A on C, we must regress C on A alone (`lm(C ~ A, dobs)`), controlling for E in the regression (`lm(C ~ A + E, dobs)`) gives us the direct effect of A on C.

---
### A Single Analysis is Usually Insuffient to Measure All Effects
.pull-left[
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-19-1.png" width="70%" />

`lm(C ~ A, dobs)`

`$c = 100+0.2a \space (p<.001)$`
]
.pull-right[
This simple 3 variable dataset requires two different regression analyses to estimate the causal effects of `$A$` on `$C$` and `$E$` on `$C$`
  
- Total effect of `$E$`, Direct effect of `$A$`:

`lm(C ~ A + E, dobs)`

`$c = 99.99+-0.93e + 0.48a \space (p<.001)$`
-  Total effect of `$A$`:
    `lm(C ~ A, dobs)`

`$c = 100+0.2a \space (p<.001)$`
  
Simply throwing all covariates into a single regression is insufficient... but this is what most machine learning models do
]
???
To get the direct effect of `$A$` and `$E$` (thereby estimating all path coefficients) we would have to regress `$E$` on `$A$`. Later slides show that we don't need to adjust for `$C$` because it is a collider. Adjusting for `$C$` would give an incorrect estimate of the effect of `$A$` on `$E$`.

---
class: center, middle

.Large[How do we know when and what to adjust for?]

---
## Paths in Causal DAGs
.pull-left[
Observational Causal DAG
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-20-1.png" width="70%" />
]
.pull-right[
A **path** is a sequence of non-intersecting adjacent edges
  - Non-intersecting means a path cannot cross a node more than once
  - Direction of the arrows doesn't matter

Examples:
  - `$A \rightarrow E$`
  - `$A \rightarrow E \rightarrow C$`
  - `$E \leftarrow A \rightarrow C$`
  
All associations are transmitted along paths,
but not all paths transmit association!
]

???
Source: https://www.ssc.wisc.edu/~felwert/causality/wp-content/uploads/2013/06/2-elwert_dags.pdf
See here for how to cite sources using refmanager package: https://github.com/yihui/xaringan/wiki/Bibliography-and-citations

---
class: center, middle
.Large[Two Kinds of Paths: **Causal** and **Non-Causal**]

---
## Causal Paths
.pull-left[
Observational Causal DAG
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-21-1.png" width="70%" />
]
.pull-right[
**Causal Path:** A path in which all arrows point away from the treatment to the outcome
 - Causal path for Treatment `$E$` and Outcome `$C$`
    * `$E \rightarrow C$`
  
 - Causal paths for Treatment `$A$` and Outcome `$C$`
    * `$A \rightarrow E \rightarrow C$`
    * `$A \rightarrow C$`
    
The **total causal effect** of a treatment on an outcome consists of association transmitted along all causal paths connecting them
]

---
## Non-Causal Paths
.pull-left[
Observational Causal DAG
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-22-1.png" width="70%" />
]
.pull-right[
**Non-Causal Path:** A path from the treatment to the outcome in which at least one arrow points back to the treatment
 - Non-Causal path for Treatment E and Outcome C
    * `$E \leftarrow A \rightarrow C$`
  
 - Non-Causal paths for Treatment `$A$` and Outcome C
    * None
    
Non-causal paths are potential spurious sources of association between treatment and outcome
]
???
Technically `$A$` cannot be a treatment, because we cannot externally manipulate age. Body Mass Index, Obesity, and Cholesterol levels are similar kinds of variables, because none are directly manipulable. This has led to a bit of feud between different groups of causal inference researchers on the question of whether it even makes sense to estimate the causal effect of non-manipulable causes. For some background on this, see the papers below, but also check out Pearl and Hernan's twitter feeds for a look at their different perspectives. Much of this centers on the need to test well-defined interventions. Obesity can only be manipulated indirectly, so why not just define a precise intervention and measure the causal effect of that intervention on some outcome of interest? Pearl argues that we still want to know the effect of obesity, because if we find that indirect changes in obesity has no effect on say life expectancy, then we might as well stop worrying about obesity, at least with respect to life expectancy.

Pearl J. Does obesity shorten life? Or is it the soda? On non-manipulable causes. Journal of Causal Inference. 2018 Sep 25;6(2).

Hernán MA, Taubman SL. Does obesity shorten life? The importance of well-defined interventions to answer causal questions. International journal of obesity. 2008 Aug 11;32(S3):S8.

Hernán MA. Does water kill? A call for less casual causal inferences. Annals of epidemiology. 2016 Oct 1;26(10):674-80.

---
### Causal and Non-Causal Paths for Treatment E and Outcome C
.pull-left[
Observational Causal DAG
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-23-1.png" width="70%" />
]
.pull-right[
Causal path:
  - `$E \rightarrow C$`
  
Non-Causal path:
  - `$E \leftarrow A \rightarrow C$`

The non-causal path is a source of confounding because it transmits spurious association between `$E$` and `$C$`

Adjusting for `$A$` in the observational data blocks this path, allowing us to use the observational data to estimate the causal effect of `$E$` on `$C$`
]

---
## Identifiability and Estimation
A causal effect is **identifiable** if the controlled (post-intervention) distribution can be estimated from data drawn from the observational (pre-intervention) distribution.

- The **Backdoor Criterion** is one set of constraints for determining whether an effect is identifiable:

- The causal effect of `$T$` on `$Y$` is **identifiable** if
we can adjust for a set of variables that

- blocks all non-causal paths between `$T$` and `$Y$`
      - without blocking any causal paths between `$T$` and `$Y$`
 
**Estimation** is the act of quantifying an identifiable causal effect from finite data

- Uses statistical estimation techniques

---
### Blocking and Unblocking Paths
All Causal DAGs are a combination of these three patterns:

.pull-left[
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-24-1.png" width="70%" />
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-25-1.png" width="70%" />
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-26-1.png" width="70%" />
]
.pull-right[
**Linear Path (or Chain)**
- Adjusting for `$E$` (a mediator) *blocks* the path between `$A$` and `$C$`

**Common Cause**
- Adjusting for `$A$` *blocks* the path between `$E$` and `$C$`

`$$\space$$`

**Common Effect**
- `$C$` is called a collider
- Unadjusted colliders *block* the path
- Adjusting for `$C$` (or a descendent of `$C$`)  **unblocks or opens** the path
]
???
In the linear chain, adjusting for a child of the mediator `$E$` will block part of the causal path from `$A$` to `$C$`. A child of a mediator is sometimes called a descending proxy. Here `$F$` is a descending proxy:

If `$F$` was a parent of `$E$` adjusting for `$F$` would not affect the path from `$A$` to `$C$`.

---
## Identifying the Total and Direct Effects of `$A$` on `$C$`
.pull-left[
Observational Causal DAG
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-28-1.png" width="70%" />
]
.pull-right[
**Total Effect of `$A$` on `$C$`**

- No adjustments needed
    - All paths from `$A$` to `$C$` are causal
        - `$A \rightarrow C$`
        - `$A \rightarrow E \rightarrow C$`
    - `lm(C ~ A, dobs)`

**Direct Effect of `$A$` on `$C$`**

- Adjusting for `$E$` blocks the path `$A \rightarrow E \rightarrow C$` leaving only the direct path `$A \rightarrow C$`
    - `lm(C ~ A + E, dobs)`
]

---
## Identifying the Total Effect of `$A$` on `$E$`
.pull-left[
Observational Causal DAG
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-30-1.png" width="70%" />
]
.pull-right[
**Total (and Direct) Effect of `$A$` on `$E$`**

- No adjustments needed
    - Causal path
        - `$A \rightarrow E$`
    - Non-causal path, blocked by collider `$C$`
        - `$A \rightarrow C \leftarrow  E$`
        - Adjusting for `$C$` would distort the effect estimate
    - `lm(E ~ A, dobs)`
]

???
Show the effects and how adjusting distorts the effect
---
## Backdoor Criterion (Pearl 1995)
A set of variables `$\{Z\}$` (possibly empty) satisfies the **backdoor criterion** relative to an ordered pair of variables `$\{X, Y\}$` in a DAG if:

1. no node in `$\{Z\}$` is a descendent of `$X$`, and
  
  2. `$\{Z\}$` blocks every path between `$X$` and `$Y$` that contain an arrow into `$X$` (the "backdoor paths")
  
If `$\{Z\}$` meets the backdoor criterion, the total causal effect of `$X$` on `$Y$` is non-parametrically identifiable given `$\{Z\}$`, such that:

$$ P(Y|do(X)) = \sum_{Z} P(Y|X,Z)P(Z)$$

The backdoor criterion recognizes that all paths that descend from `$X$` are either causal or blocked
---

## Multiple Adjustment Sets
.pull-left[
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-31-1.png" width="70%" />
]
.pull-right[
Adjustment sets for `$X \rightarrow Y$`:

```
##  { W1, W2, Z2 }
##  { V, W1, W2 }
##  { W1, W2, Z1 }
```

Adjusting for any one of these sets of variables eliminates confouding for the causal effect of `$X$` on `$Y$`

For a linear model this means regressing `$Y$` on `$X$`, including as covariates only one set of these variables

In R, any of these statements will estimate the total effect of `$X$` on `$Y$` from observational data `obsdata`:

```r
lm(obsdata, Y ~ X + W1 + W2 + Z2)
lm(obsdata, Y ~ X + V + W1 + W2)
lm(obsdata, Y ~ X + W1 + W2 + Z1)
```
]

---
# Adjustment Sets for `$X \rightarrow Y$`

![](overview_causal_inference_files/figure-html/unnamed-chunk-34-1.png)
???
Bold edges are unadjusted, light edges are adjusted

The backdoor criterion implicitly prevents adjusting for children of mediators. For instance, suppose we want to determine the causal effect of `$X$` on `$Y$` in the model:

`$$X \rightarrow Z \rightarrow Y$$`
`$$Z \rightarrow Z_2$$`
where `$Z$`, a mediator, causes `$Z_2$`. It is clear that adjusting for `$Z$` would block the path between `$X$` and `$Y$`, but adjusting for `$Z_2$` would partially block the path.

---
exclude: FALSE
# Frontdoor Adjustment Criterion
.pull-left[
U unmeasured: Cannot block backdoor path from `$X \rightarrow Y$`

<img src="overview_causal_inference_files/figure-html/unnamed-chunk-35-1.png" width="70%" />
]
.pull-right[
`$X \rightarrow Y$` is still identifiable using a two step process:

Step 1. Identify `$X \rightarrow Z$`:

* Backdoor path blocked by collider `$Y$`
  
`$$X \leftarrow U \rightarrow Y \leftarrow Z$$`
  * In R: `lm(obsdata, Z ~ X)`
  
Step 2. Identify `$Z \rightarrow Y$`:

* Backdoor path blocked by adjusting for `$X$`

`$$Z \leftarrow X \leftarrow U \rightarrow Y$$`
  * In R: `lm(obsdata, Y ~ Z + X)`
]
???
Since `$U$` is unmeasured, we cannot adjust for it. However, in this case, the frontdoor adjustment criterion allows us to identify the causal effect of `$X$` on `$Y$` in two steps.

---
exclude: false
## Frontdoor Adjustment Criterion (Pearl 1995)
A set of variables `$\{Z\}$` satisfies the **frontdoor criterion** relative to an ordered pair of variables `$\{X, Y\}$` in a DAG if:

1. `$\{Z\}$` intercepts all directed paths from `$X$` to `$Y$`,
  
  2. there is no backdoor path between `$X$` and `$Z$`,
  
  3. every backdoor path between `$Z$` and `$Y$` is blocked by `$X$`
  
If `$\{Z\}$` meets the frontdoor criterion, the causal effect of `$X$` on `$Y$` is identifiable given `$\{Z\}$`, such that:

`$$P(y|do(x)) = \sum_{z} P(z|x)\sum_{x'}P(y|x', z)P(x')$$`

`$x$` is the value of `$X$` in `$do(x)$`, `$x'$` refers to all values of `$X$`

---
exclude: true
## Instrumental Variables
Instrumental variables are those that only affect the treatment, with no relationship to anything else

---
exclude: false
# Identifying Covariate Specific Effects
Suppose a drug `$D$` affects `$C$`, and that gender `$G$` affects who takes the drug.

.pull-left[
What is the effect of `$E$` on `$C$` when we *observe* `$D = d$`?
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-36-1.png" width="70%" />
]
.pull-right[
Estimate `$P(C=c|do(E=e), D=d)$`

Must use an adjustment set `$S$`, such that `$S \cup D$` blocks all backdoor paths from `$E$` to `$C$`.

No need to block backdoor path from `$D$` to `$C$`.

For this graph, `$S = \{A\}$` and and `$S \cup D = \{A, D\}$`

Regression: `lm(obsdata, C ~ E + A + D)`

Mathematically:

`$$\begin{aligned} P(C=c&|do(E=e), D=d) = \\  &\sum_S P(C=c|E=e, D=d, S=s)P(S=s|D=d) \end{aligned}$$`

]
???
Note that the summation in the adjustment formula is over `$S$`, not `$S \cup D$`. `$S$` is the set of all the other variables needed to block the backdoor paths from `$E$` to `$C$`.

As a notational note, when you see a statement such as `$P(S=s)$` and `$S$` contains more than one variable, it is just shorthand for `$P(S_1=s_1, S_2=s_2...)$`. In this example, because `$S=\{A,D\}$` `$P(S=s) = P(A=a, D=d)$`.

We don't want to block the backdoor path from `$D$` to `$C$` here, because the query is asking for the effect of `$E$` on `$C$` when we intervene on `$E$` and then in the resulting interventional distribution observe `$D=d$`.

In contrast, if we just want to identify `$P(C=c|do(E=e))$` we have:

`$$P(C=c|do(E=e)) = P(C=c|E=e, S=s)P(S=s)$$`

where `$S$` is a valid adjustment set that blocks the backdoor paths from `$E$` to `$C$`.

The basic idea is that when we look at the interventional distribution (resulting from adjusting for `$S$`), we must stratify by `$D$` to compute the covariate-specific effect, which means we are also adjusting for `$D$`. Thus we have to make sure that adjusting for `$D$` does not open any backdoor paths for the effect from `$E$` to `$C$`.

To see this, consider adding high blood pressure `$B$` to the graph with the paths `$E \rightarrow B \leftarrow D$`, meaning that both `$E$` and `$D$` affect `$B$`. If we ask how `$D$` affects `$C$` among those with high blood pressure, we must adjust for `$G$` to block the backdoor path `$D \leftarrow G \rightarrow C$` and also `$B$`, a collider, which opens the backdoor path `$D \rightarrow B \leftarrow E \rightarrow C$`. As a result, we need to add `$E$` to the adjustment set, giving

`$$S = \{G, E\}$$`

and

`$$P(C=c|do(D=d), B=b) = P(C=c|D=d, B=b, G=g, E=e)P(B=b, G=g|B=b)$$`

---
exclude: false
## Identifying the Effects of Multiple Interventions
What is the effect of simultaneously intervening on `$E$` and `$D$`?
.pull-left[
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-37-1.png" width="70%" />
]
.pull-right[
Estimate `$P(C=c|do(E=e, D=d))$`

Must use an adjustment set `$S$` that blocks all backdoor paths from `$E$` to `$C$` and `$D$` to `$C$`. For this graph:

`$$S = \{A, G\}$$`

Regression: `lm(C ~ E + A + D + G)`

Mathematically:

`$$\begin{aligned} P(C=c&|do(E=e, D=d)) = \\  &\sum_S P(C=c|E=e, D=d, S=s)P(S=s) \end{aligned}$$`
]

---
## Confounding is a Causal Concept

* The data alone are insufficient to identify confounders or control for confouding
* Without a causal model, observational data is limited to associational models that do not tell us how to intervene
  + This includes all common machine learning and statistical approaches
  + Example: If an associational predictive model finds a few highly predictive "risk factors" we cannot assume that intervening on those risk factors will decrease risk.
* Associational predictive models are still useful if we already have interventions that are known to work
  + If we know that a treatment works if given earlier in the course of a disease, better predictive models can tell us who to treat
  + Variables that increase the predictive power of an associational model may include effects of the outcome, such as symptoms of a disease you are trying to predict

---
class: center, middle, Large

Causal Inference Requires a Causal Model,

But...

How Do we Know if Our Model is Correct?

---
class: center, middle
# Part III: Model Evaluation

---
# Part III Learning Objectives: Model Evaluation
- Identify two different approaches for evaluating causal models
- Describe the advantages and disadvantages of each approach
- Define what constitutes an equivalence class of causal DAGs

---
# Two Approaches to Model Evaluation
Local fit tests

- Tests of model-implied conditional independence assumptions

Global fit tests

- Model chi-square: comparison of model vs. observed covariance matrices

- RMSEA: Root Mean Square Error of Approximation

- CFI: Comparative fit index

- SRMSR: Standaridzed Root Mean Square Residual
???
From: Kline RB. Principles and practice of structural equation modeling. Guilford publications; 2015 Nov 3.
---
## Model Evaluation: Local Fit Tests
Causal DAG's imply independence relations

.pull-left[
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-39-1.png" width="70%" />
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-40-1.png" width="70%" />
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-41-1.png" width="70%" />
]
.pull-right[
**Linear Path (or Chain)**

- `$A \perp\!\!\!\perp C | E$`

**Common Cause**

- `$E  \perp\!\!\!\perp  C | A$`

`$$\space$$`
`$$\space$$`

**Common Effect**

- `$A  \perp\!\!\!\perp  E$`
  - `$A  \not\!\perp\!\!\!\perp  E | C$`
]

---
## Example: Age, Gender, BMI and Cholesterol
.small[Causal DAG Implied by Gostynski M, Gutzwiller F, Kuulasmaa K, Döring A, Ferrario M, Grafnetter D, Pajak A. [**Analysis of the relationship between total cholesterol, age, body mass index among males and females in the WHO MONICA Project.**](https://www.nature.com/articles/0802714) *International Journal of Obesity.* 2004 Aug;28(8):1082.]

.pull-left[
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-42-1.png" width="70%" />
]

.pull-right[
This Causal DAG implies the following conditional independencies

.scroll-box-8[

```
bmi _||_ chdt
bmi _||_ chrx
bmi _||_ eage | height, weight
bmi _||_ high
bmi _||_ sex | height, weight
chdt _||_ chrx | high
chdt _||_ eage
chdt _||_ height
chdt _||_ sex
chdt _||_ weight
chol _||_ height | bmi, eage, sex
chol _||_ high | chdt, chrx
chol _||_ weight | bmi, eage, sex
chrx _||_ eage
chrx _||_ height
chrx _||_ sex
chrx _||_ weight
eage _||_ height
eage _||_ high
eage _||_ sex
height _||_ high
high _||_ sex
high _||_ weight
```
]

Given data on these variables, we can test for these statistical relationships.
]
???
The tests shown here form a basis set for this graph, even though I did not tell dagitty to return the basis set (using option type="basis.set"). Specifying this option gives a set that when passed to localTests returns a list with p-values that are not easily accessible for later tests. The 'piecewiseSEM' package appears to have better functions for calculating and then testing basis sets. It also has a function 'fisherC' to directly calculate the C statistic.

---
### Testing Implied Independencies with Observed Data

.pull-left[
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-44-1.png" width="70%" />
]

.pull-right[
Independence tests for all implied independencies based on 9006 participants:

<div id="htmlwidget-4ba71909679e5032b68b" style="width:100%;height:auto;" class="datatables html-widget"></div>
<script type="application/json" data-for="htmlwidget-4ba71909679e5032b68b">{"x":{"filter":"none","fillContainer":false,"data":[["bmi _||_ chdt","bmi _||_ chrx","bmi _||_ eage | height, weight","bmi _||_ high","bmi _||_ sex | height, weight","chdt _||_ chrx | high","chdt _||_ eage","chdt _||_ height","chdt _||_ sex","chdt _||_ weight","chol _||_ height | bmi, eage, sex","chol _||_ high | chdt, chrx","chol _||_ weight | bmi, eage, sex","chrx _||_ eage","chrx _||_ height","chrx _||_ sex","chrx _||_ weight","eage _||_ height","eage _||_ high","eage _||_ sex","height _||_ high","high _||_ sex","high _||_ weight"],[-1.23067725357363,-1.23355869140642,0.000786009396347763,-1.34320860032269,0.0229297239733698,0.985337536852835,-0.00694528710948228,0.0749577248650493,0.0376077990917615,-0.00181798716979704,-0.347444740387063,-1.18673719938979,-0.00238351457247724,-0.00693142715608561,0.0724766326464175,0.0378092096767193,-0.00182787137919673,-22.4348307179151,-6.26761976706577,-0.277776000625562,0.00856308919789195,0.0244429516365817,-0.00175429520713193],[4.8663369267197e-19,4.55255798844105e-19,0.487097674672083,1.19787586564446e-21,0.487097674672083,0,2.33933984958371e-85,0.379683296779327,9.13169214277496e-06,3.21107129605543e-11,0.325854832361472,2.99376097098296e-16,0.487097674672083,3.49633547322941e-85,0.379683296779327,8.58920696631395e-06,2.51742189430978e-11,8.34304340270124e-79,1.57379463631955e-86,0.487097674672083,0.0184536889051569,0.0101011426233696,6.07231435788752e-11]],"container":"<table class=\"nowrap hover\">\n  <thead>\n    <tr>\n      <th> <\/th>\n      <th>estimate<\/th>\n      <th>p.value<\/th>\n    <\/tr>\n  <\/thead>\n<\/table>","options":{"pageLength":3,"dom":"tp","order":[[2,"asc"]],"columnDefs":[{"className":"dt-right","targets":[1,2]},{"orderable":false,"targets":0}],"autoWidth":false,"orderClasses":false,"lengthMenu":[3,10,25,50,100],"rowCallback":"function(row, data) {\nDTWidget.formatRound(this, row, data, 1, 2, 3, ',', '.');\nDTWidget.formatRound(this, row, data, 2, 2, 3, ',', '.');\n}"}},"evals":["options.rowCallback"],"jsHooks":[]}</script>
]

???
The table is sorted in increasing order by `p.values`

`p.values` were corrected for multiple comparisons using the Holm-Bonferroni method

The null hypothesis is that the estimate is 0, which would indicate independence, so if `$p < .05$` we can reject the null, meaning that the indpendence implication is unlikely to be true.

See Figure 1 in http://johannes-textor.name/papers/2017-ije.pdf for details (Textor J, van der Zander B, Gilthorpe MS, Liśkiewicz M, Ellison GT. Robust causal inference using directed acyclic graphs: the R package ‘dagitty’. *International journal of epidemiology.* 2016 Dec 1;45(6):1887-94.)

Tests for independence are linear in the dagitty package. Distance Correlation can detect non-linear independence For example:

```r
# Too slow to run each time slides are processed
library(energy) # provides test for marginal independence using distance correlation

# Tests show probability of independence
# Low p values indicate dependence

#  Distance correlation is computationally intensive $O(n^2)$ and memory intensive, so use a random sample of data
monicasamp <- sample_n(monica, 1000)
dcor.ttest(monica$eage, monica$sex) # marginally independent

# Independence under partial correlation (whether distance or linear) is not identical to conditional independence. 
# The CDCSIS package (below) tests for conditional independence using distance correlation, whereas the energy package (above) only tests for partial distance correlation. 
# If all variables are multivariate gaussian, the partial linear correlation is 0 if and only if  X and Y are conditionally linearly independent given Z, but otherwise this is not true. 
# See the following paper for more details on the relationship between conditional independence of partial correlation: https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1467-842X.2004.00360.x

# See section 4.3 of (http://real.mtak.hu/44934/1/pdcov.pdf) Székely GJ, Rizzo ML. Partial distance correlation with methods for dissimilarities. The Annals of Statistics. 2014;42(6):2382-412.

# Test independence under partial correlation independence hypothesis using distance correlation. 
pdcor.test(monicasamp$bmigrp, monicasamp$weight, monicasamp$bmi, R=99) # Dependent although model implies independence

library(cdcsis) # Provides cdcsis and cdcsis.test for conditional distance correlation

# compute conditional distance correlation 
cdcsis(as.matrix(monicasamp$bmigrp), monicasamp$weight, as.matrix(monicasamp$bmi), threshold = 1) # must give threshold here as 1 for this data
# Test conditional independence hypothesis using distance correlation
cdcov.test(as.matrix(monicasamp$bmigrp), monicasamp$weight, as.matrix(monicasamp$bmi)) # Dependent at the .05 level, but not .01
```

---
# Coefficients where `$p < .05$`

.pull-left[
![](overview_causal_inference_files/figure-html/unnamed-chunk-47-1.png)
]

.pull-right[
The data suggests that `$eage$` and `$height$`, and `$eage$` and `$high$` are *not* marginally independent

This contradicts our model

Any ideas as to why `$eage$` and `$high$` are not marginally independent?
]

???
`$high$` indicates that a patient was told that he or she had high cholesterol. This means that  `$high$` is dependent on a past measurement of high cholesterol, which itself is likely tied to past age, weight, etc. A more accurate model would have these past values along with edges leading to the present values.
---
## Add `$eage \rightarrow height$` and `$eage \rightarrow high$` and Retest

.pull-left[
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-48-1.png" width="70%" />
]

.pull-right[
Coefficients where `$p < .05$`

![](overview_causal_inference_files/figure-html/unnamed-chunk-49-1.png)
]
???
There are still many discrepencies here

---
exclude: false
## Summarizing Independence Tests: Fisher's C
- Statistical test of the set of independence test results

`$$C = -2\sum \ln p_i$$`
 - `$p_i$` are the `$p$`-values of all tests of conditional independence for the **basis set**
- **Basis Set**: the smallest set of independence relations implied by a DAG
- Fisher's C requires a basis set constructed by listing "each unique pair of nonadjacent
vertices `$(v_i, v_j)$` and then forming the conditioning set of this pair by listing all other vertices in the DAG that are parents of either `$v_i$` or of `$v_j$`.".fn[1]

- `$C$` has a `$\chi^2$` distribution with `$2k$` degrees of freedom, where `$k$` is the number of elements in the basis set

- `$p \geq .05$` is good
 - If `$p < .05$` reject model, consider alternatives: more links, different structure, etc.

- For the WHO MONICA DAG: `$C$` = \infty{}, `$p$` = 0

.footnote[[1] Shipley, B. A new inferential test for path models based on directed acyclic graphs. *Structural Equation Modeling*. 2000 Jun 1;7(2):206-18.]
???
See Shipley: A New Inferential Test for Path Models Based on Directed Acyclic Graphs: https://pdfs.semanticscholar.org/23e5/29d073a66c314f19900e5e1e7fc510453812.pdf

The basis set required for this test (according to Shipley is): "To obtain the basis set Bø from a DAG, simply list each unique pair of nonadjacent
vertices (vi, vj) and then form the conditioning set of this pair by listing all other vertices in the DAG that are parents of either vi or of vj."

To calculate `$C$` and the `$\chi^2$` `$p$`-value in R, given that the `$p$`-values for the WHO MONICA DAG are in `r$p.value`:

```r
C = -2*sum(log(r$p.value))
k = length(r$p.value) # Number of tests in basis set
p = 1 - pchisq(C, 2 * k)
cat("p = ", p)
```

```
## p =  0
```

The implied independencies shown in earlier slides happen to be a  basis set for this graph (which is not guaranteed for all graphs when the function is called without type="basis.set"). 'dagitty' can produce a basis set using the option type="basis.set" as shown here, but when supplied with the resulting implications, its localTests function did not return a value that allows easy extraction of the p values, so I used the basis set shown on the previous slide.

There can be more than one basis set for a given DAG, but not 
all basis sets are mutually independent in finite data samples.

Section 3.4 of

Shipley B. Cause and correlation in biology: a user's guide to path analysis, structural equations and causal inference with R. Cambridge University Press; 2016 Apr 18. discusses these issues and includes a description of Shipley's method for producing a basis set that is independent in finite samples. This is also described in the paper:

Shipley B. A new inferential test for path models based on directed acyclic graphs. Structural Equation Modeling. 2000 Jun 1;7(2):206-18. https://pdfs.semanticscholar.org/23e5/29d073a66c314f19900e5e1e7fc510453812.pdf

---
# Limitations
- Most packages only detect (lack of) linear dependence
 - Independent variables are guaranteed to have `$0$` correlation
 - But `$0$` correlation does not imply independence when the relationship is nonlinear
 - A Partial correlation of `$0$` (for conditional independence) implies conditional independence only when the joint distribution of the tested variables is multinormal
 
- Distance correlation (Szekely, et al. 2007) and conditional distance correlation (Wang, et al., 2015) can detect nonlinear dependence
 - But complexity is at worst `$\mathcal{O}(n^2)$` and at best `$\mathcal{O}(n\log n)$` (Chaudhuri and Hu, 2019)
 
???
 Székely GJ, Rizzo ML, Bakirov NK. Measuring and testing dependence by correlation of distances. The annals of statistics. 2007;35(6):2769-94.
 
  Wang X, Pan W, Hu W, Tian Y, Zhang H. Conditional distance correlation. Journal of the American Statistical Association. 2015 Oct 2;110(512):1726-34.
 
 Chaudhuri A, Hu W. A fast algorithm for computing distance correlation. Computational Statistics & Data Analysis. 2019 Jul 1;135:15-24.
 
---
## Global Fit Tests

.pull-left-65[
.scroll-box-20[
All variables standardized before analysis

```
lavaan 0.6-4.1417 ended normally after 75 iterations

Optimization method                           NLMINB
  Number of free parameters                         20

Number of observations                          9006

Estimator                                         ML
  Model Fit Test Statistic                   28601.806
  Degrees of freedom                                19
  P-value (Chi-square)                           0.000

Model test baseline model:

Minimum Function Test Statistic           130110.094
  Degrees of freedom                                33
  P-value                                        0.000

User model versus baseline model:

Comparative Fit Index (CFI)                    0.780
  Tucker-Lewis Index (TLI)                       0.618

Loglikelihood and Information Criteria:

Loglikelihood user model (H0)             10583937.038
  Loglikelihood unrestricted model (H1)     -17698.358

Number of free parameters                         20
  Akaike (AIC)                              -21167834.075
  Bayesian (BIC)                            -21167691.962
  Sample-size adjusted Bayesian (BIC)       -21167755.519

Root Mean Square Error of Approximation:

RMSEA                                          0.409
  90 Percent Confidence Interval          0.405  0.413
  P-value RMSEA <= 0.05                          0.000

Standardized Root Mean Square Residual:

SRMR                                           0.019

Parameter Estimates:

Information                                 Expected
  Information saturated (h1) model          Structured
  Standard Errors                             Standard

Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)
  height ~                                            
    eage             -0.019    0.001  -27.675    0.000
    sex              -1.357    0.015  -90.876    0.000
  weight ~                                            
    height            0.492    0.012   39.602    0.000
    eage              0.019    0.001   22.077    0.000
    sex              -0.159    0.024   -6.512    0.000
  bmi ~                                               
    weight            1.149    0.001  843.146    0.000
    height           -0.656    0.001 -481.813    0.000
  hychol ~                                            
    bmi               0.071    0.010    6.937    0.000
    sex              -0.008    0.020   -0.414    0.679
    eage              0.017    0.001   17.014    0.000
    chdt              0.195    0.030    6.617    0.000
    chrx             -0.406    0.030  -13.770    0.000
  chdt ~                                              
    high              2.725    0.007  378.606    0.000
  chrx ~                                              
    high              2.726    0.007  381.041    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)
   .height            0.501    0.007   67.104    0.000
   .weight            0.697    0.010   67.104    0.000
   .bmi               0.012    0.000   67.104    0.000
   .hychol            0.893    0.013   67.104    0.000
   .chdt              0.059    0.001   67.104    0.000
   .chrx              0.058    0.001   67.104    0.000
```
]
]

.pull-right-35[
Recommended levels for global fit tests

- Model `$\chi^2$` with df and `$p$`-value
 - prefer `$p \geq .05$`
- Comparative Fit Index
 - prefer CFI `$> 0.90$`
- Root mean square error of Approximation
 - prefer lower 90%CI to be `$< .05$`
- Standardized Root Mean Square Residual
 - prefer SRMR `$< 0.10$`
]
???
Pearl argues against global fit tests because they rarely tell you where your model might be wrong. In addition, many different models can often fit the same data. He also points out that for estimating specific effects, not all of the model needs to be correct. As long as the local independence tests are valid for the effect of interest, you can still use the effect estimates.
 
---
### Visualize Mismatch between Model and Data Covariance Matrices
This shows observed - model-implied correlations
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-54-1.png" width="70%" />
---
exclude: false
## Examine Modification Indices
MI Indicates possible improvement in model test score

```
##       lhs op    rhs       mi    epc sepc.lv sepc.all sepc.nox
## 39 hychol ~~   chdt   64.346  0.028   0.028    0.122    0.122
## 40 hychol ~~   chrx   64.347  0.028   0.028    0.121    0.121
## 41   chdt ~~   chrx 8623.979  0.057   0.057    0.979    0.979
## 52 weight  ~   high   25.967 -0.129  -0.129   -0.046   -0.129
## 61 hychol  ~   high   64.351 -1.291  -1.291   -0.458   -1.287
## 62   chdt  ~ height   20.421 -0.012  -0.012   -0.012   -0.012
## 65   chdt  ~ hychol   35.382 -0.022  -0.022   -0.022   -0.022
## 66   chdt  ~   chrx 8623.983  0.984   0.984    0.984    0.984
## 68   chdt  ~    sex   51.703  0.037   0.037    0.018    0.037
## 69   chrx  ~ height   23.030 -0.012  -0.012   -0.012   -0.012
## 72   chrx  ~ hychol  186.354  0.050   0.050    0.050    0.050
## 73   chrx  ~   chdt 8623.958  0.973   0.973    0.973    0.973
## 75   chrx  ~    sex   54.104  0.038   0.038    0.019    0.038
```

The highest MI involved adding an undirected edge between `$chdt$` and `$chrx$`, indicating an unmeasured common cause.

---
## Age, Exercise, Cholesterol Model Implies No Independence Relations
.pull-left[
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-56-1.png" width="70%" />
]
.pull-right[

```r
print( impliedConditionalIndependencies( gobs ) )
```
* C is a collider between `$A$` and `$E$`, but `$A \rightarrow E$` **shields** the collider, rendering `$A$` and `$E$` dependent even when `$C$` is not conditioned on

There are no implied independence relationships to test.
]

---
## Independence (d-separation) Equivalence
.pull-left[
Two Causal DAGs over the same set of variables are independence equivalent iff they have:

* the same adjacencies (edges between variables ignoring direction)
* the same unshielded colliders (any two nodes pointing into the collider are not adjacent)
  * In graphs 1 and 3, `$C$` is a *shielded* collider, because `$A$` and `$E$` have an edge between them
  * If we deleted the edge between `$A$` and `$E$`, then `$C$` would be an unshielded collider

These graphs are all independence equivalent.  (Verma and Pearl, 1988)
]
.pull-right[
![](overview_causal_inference_files/figure-html/unnamed-chunk-58-1.png)
]
???
This concept is explained in detail in the following lecture at around 28 minutes:

From https://www.youtube.com/watch?v=TISSNwWDfw4&list=PLO5mmwQolPRX858CyOOIHqYnmdzlHjIgS&index=8

(CCD Summer short course 2016:Day 2 Part 1)

---
exclude: true
### Completed Partially Directed Acyclic Graph (CPDAG)
.pull-left[
![](overview_causal_inference_files/figure-html/unnamed-chunk-59-1.png)
]
.pull-right[
A CPDAG represents an equivalance class of independence equivalent graphs

* A directed edge is shared by all graphs in the class
* An undirected edge is reversible as long as no cycles or additional unshielded colliders are introduced
]

---
exclude: true
### Global Tests of AEC Model are Uninformative
There are 5 free parameters and 0 degrees of freedom.

.scroll-box-18[

```
## lavaan 0.6-4.1417 ended normally after 26 iterations
## 
##   Optimization method                           NLMINB
##   Number of free parameters                          5
## 
##   Number of observations                         10000
## 
##   Estimator                                         ML
##   Model Fit Test Statistic                       0.000
##   Degrees of freedom                                 0
## 
## Parameter Estimates:
## 
##   Information                                 Expected
##   Information saturated (h1) model          Structured
##   Standard Errors                             Standard
## 
## Regressions:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   E ~                                                                   
##     A                 0.300    0.001  297.457    0.000    0.300    0.948
##   C ~                                                                   
##     A                 0.479    0.016   30.635    0.000    0.479    0.879
##     E                -0.931    0.049  -18.835    0.000   -0.931   -0.540
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .E                 1.012    0.014   70.711    0.000    1.012    0.102
##    .C                24.733    0.350   70.711    0.000   24.733    0.836
```
]

---
exclude: true
### Age, Sex, Gender, BMI, and Cholesterol
.pull-left[
Hypothesized Graph

<img src="overview_causal_inference_files/figure-html/unnamed-chunk-61-1.png" width="70%" />
]
.pull-right[
CPDAG

![](overview_causal_inference_files/figure-html/unnamed-chunk-62-1.png)
]

---
class: middle, center
# Part IV: Causal Discovery from Observational Data

---
# Part IV Learning Objectives: Causal Discovery from Observational Data

- Describe how conditional independence tests of a dataset constrains the possible causal DAGs that may have generated the data
- Describe the steps of the PC causal discovery algorithm

---
# Inferring Causal Structure from Data

.center[**Causal DAG `\$\Rightarrow\$` Independence Relations**]

.pull-left[
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-63-1.png" width="70%" />
]

.pull-right[
.scroll-box-16[

```
bmi _||_ chdt | high
bmi _||_ chdt | eage
bmi _||_ chdt | height, weight
bmi _||_ chrx | high
bmi _||_ chrx | eage
bmi _||_ chrx | height, weight
bmi _||_ eage | height, weight
bmi _||_ high | eage
bmi _||_ high | height, weight
bmi _||_ sex | height, weight
chdt _||_ chrx | high
chdt _||_ eage | high
chdt _||_ height | eage
chdt _||_ height | high
chdt _||_ sex
chdt _||_ weight | eage
chdt _||_ weight | high
chol _||_ height | bmi, eage, sex
chol _||_ high | chdt, chrx, eage
chol _||_ weight | bmi, eage, sex
chrx _||_ eage | high
chrx _||_ height | eage
chrx _||_ height | high
chrx _||_ sex
chrx _||_ weight | eage
chrx _||_ weight | high
eage _||_ sex
height _||_ high | eage
high _||_ sex
high _||_ weight | eage
```
]
]

.center[**Causal DAGS `\$\Leftarrow\$` Independence Relations**]

---
# PC Algorithm.fn[1]
1. Adjacency Phase
    - Determine which variables are adjacent
1. Orientation Phase
    - Orient direction of arrows if possible

.footnote[[1] Spirtes and Glymour, 1991]

---
### PC Algorithm: Adjacency Phase

`$X$` and `$Y$` are not adjacent if they are conditionally independent given any subset of variables that does not contain `$X$` and `$Y$`

- Begin with a fully connected graph
- Remove edge between `$X$` and `$Y$` if `$X \perp\!\!\!\perp Y | \text{ any set } S$`
    - Begin with the empty set and test all connected pairs for marginal independence `$X \perp\!\!\!\perp Y$`
        - Remove edges for any pair that is independent 
    - For any remaining connected pair, test conditional independence vs. each single other variable, ie., `$S$` of size 1
        - Remove edge between `$X$` and `$Y$` if `$X \perp\!\!\!\perp Y | S \text{ of size 1}$`
    - Repeat for `$S$` of size 2, 3, etc.

---
background-image: url(PCAlignmentPhaseExample.png)
background-size: contain
.footnote[From https://www.ccd.pitt.edu/wp-content/uploads/2017/02/CCD_Summer_Course_2016_Day3_morning.pdf]

---
background-image: url(PCOrientationRules.png)
background-size: contain
.footnote[From https://www.ccd.pitt.edu/wp-content/uploads/2017/02/CCD_Summer_Course_2016_Day3_morning.pdf]
???
X -- Y -- Z, X and Z must not be adjacent. If Y is not in S, then X and Z, then Y is a collider for X and Z. If Y separates X and Z, then we cannot orient the edges (other than to say that Y is not a collider)

---
background-image: url(PCOrientationPhaseExample.png)
background-size: contain
.footnote[From https://www.ccd.pitt.edu/wp-content/uploads/2017/02/CCD_Summer_Course_2016_Day3_morning.pdf]

---
exclude: true
## PC Algorithm: Adjacency Phase Example
.pull-left[
Generative DAG
![](overview_causal_inference_files/figure-html/unnamed-chunk-65-1.png)

Begin with: 
]
.pull-right[
Independencies

`\begin{align}
X1 \perp\!\!\!\perp X2 & \\
X1 \perp\!\!\!\perp X4 &\mid X3 \\
X2 \perp\!\!\!\perp X4 &\mid X3 \\
\end{align}`

![](overview_causal_inference_files/figure-html/unnamed-chunk-66-1.png)
]

---
exclude: true
### Results of the PC Algorithm (Spirtes and Glymour, 1991) On The WHO Monica Dataset

.pull-left[
![](overview_causal_inference_files/figure-html/unnamed-chunk-67-1.png)
]

.pull-right[
Graph implied by [Nature paper]
![](overview_causal_inference_files/figure-html/unnamed-chunk-68-1.png)
]

---
## Results of PC Algorithm on the WHO Dataset
.pull-left[
<div id="htmlwidget-8168f8c9cf786573c299" style="width:504px;height:504px;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-8168f8c9cf786573c299">{"x":{"diagram":"digraph g {\n \"chol\" -> \"eage\" [arrowtail=none, arrowhead=none]; \n \"bmi\" -> \"weight\" [arrowtail=none, arrowhead=normal]; \n \"eage\" -> \"height\" [arrowtail=none, arrowhead=normal]; \n \"bmi\" -> \"eage\" [arrowtail=none, arrowhead=none]; \n \"chdt\" -> \"high\" [arrowtail=none, arrowhead=none]; \n \"sex\" -> \"weight\" [arrowtail=none, arrowhead=normal]; \n \"bmi\" -> \"chol\" [arrowtail=none, arrowhead=none]; \n \"chrx\" -> \"high\" [arrowtail=none, arrowhead=none]; \n \"height\" -> \"weight\" [arrowtail=none, arrowhead=normal]; \n \"height\" -> \"sex\" [dir=both, arrowtail=normal, arrowhead=none]; \n \"chol\" -> \"high\" [arrowtail=none, arrowhead=none]; \n \"chdt\" -> \"chrx\" [arrowtail=none, arrowhead=none]; \n}","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>
]

.pull-right[
Hypothesized DAG
![](overview_causal_inference_files/figure-html/unnamed-chunk-70-1.png)
]

???
The PC algorithm is one of the first causal discovery algorithms. As you can see from the inferred graph, many of the arrows are incorrect and some edges are not directional, meaning the algorithm could not orient the edge.

One limitation of PC (and most other algoirithms) is that the independence tests assume linear relationships. As a result, the algorithm will mistake nonlinearly dependent variables as independent.

See: Spirtes P, Glymour C. An algorithm for fast recovery of sparse causal graphs. Social science computer review. 1991 Apr;9(1):62-72.
---
## Adding Background Knowledge Improves Discovery

```r
# List of forbidden directed edges
forbid <- list(c('chol', 'bmi'), c('eage', 'bmi'), c('sex', 'bmi'))

# List of required directed edges
require <- list(c('height', 'bmi'), c('weight', 'bmi'))

# Forbid edges between eage and sex
forbiddenWithin <- c('sex', 'eage')
class(forbiddenWithin) <- 'forbiddenWithin'

# Add Temporal constraints
temporal <- list(forbiddenWithin, c('height', 'weight', 'chrx', 'chdt', 'high'), c('bmi', 'chol'))

prior <- priorKnowledge(requiredirect = require, addtemporal = temporal, forbiddirect = forbid)
```
???
Since bmi is defined only by bmi, we forbid other variables from causing it. We could likewise forbid the two other defined variables in the dataset, eageg and hychol, but the algorithm works fine as is.

The temporal constraints indicate that lower tiers cannot have any directed edges to higher tiers. For instance, `bmi` and `chol` can have directed edges to `bmigrp` and `hychol`, as well as between themselves, but cannot have directed edges to the other variables that appear before them in the temporal list.
---

# PC Algorithm with Knowledge
.pull-left[
<div id="htmlwidget-e36a7fc19f7156833178" style="width:504px;height:504px;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-e36a7fc19f7156833178">{"x":{"diagram":"digraph g {\n \"chol\" -> \"eage\" [dir=both, arrowtail=normal, arrowhead=none]; \n \"bmi\" -> \"weight\" [dir=both, arrowtail=normal, arrowhead=none]; \n \"chol\" -> \"weight\" [dir=both, arrowtail=normal, arrowhead=none]; \n \"eage\" -> \"height\" [arrowtail=none, arrowhead=normal]; \n \"chdt\" -> \"high\" [arrowtail=none, arrowhead=none]; \n \"sex\" -> \"weight\" [arrowtail=none, arrowhead=normal]; \n \"chrx\" -> \"high\" [arrowtail=none, arrowhead=none]; \n \"eage\" -> \"weight\" [arrowtail=none, arrowhead=normal]; \n \"height\" -> \"weight\" [arrowtail=none, arrowhead=none]; \n \"height\" -> \"sex\" [dir=both, arrowtail=normal, arrowhead=none]; \n \"high\" -> \"sex\" [dir=both, arrowtail=normal, arrowhead=none]; \n \"chol\" -> \"high\" [dir=both, arrowtail=normal, arrowhead=none]; \n \"eage\" -> \"high\" [arrowtail=none, arrowhead=normal]; \n \"chdt\" -> \"chrx\" [arrowtail=none, arrowhead=none]; \n \"bmi\" -> \"height\" [dir=both, arrowtail=normal, arrowhead=none]; \n}","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>
]

.pull-right[
Causal discovery from observational data is difficult

Adding background knowledge helps, but there is no magic here.

The same algorithm, with different settings can produce a different graph.

There are many different algorithms to choose from. 
]

---
exclude: true
## Adding Knowledge: Required Edges

`TRUE` means the pair of variables must be connected by an edge

---
exclude: true
## Adding Knowledge: Forbidden Edges

A `$1$` means the row variable (e.g., `height`) must not have direct edge to the column variable (e.g., `bmi`)

---
exclude: true
### Results of the PC Algorithm With Background Knowledge

.pull-left[

]

.pull-right[
Graph implied by [Nature paper]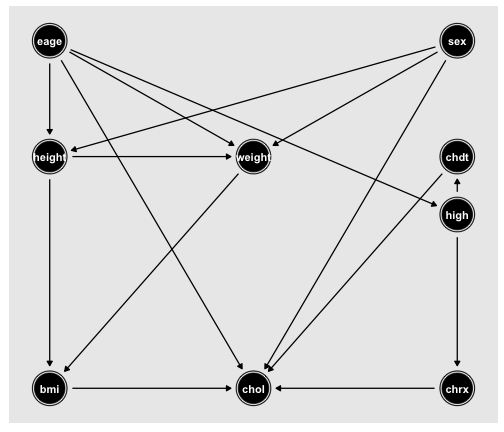
![](overview_causal_inference_files/figure-html/unnamed-chunk-76-1.png)
]

---
class: center, middle

## Part V: Counterfactual Reasoning

---
## Counterfactual Reasoning Example 
- Joe is `$60$` years old, exercised `$10$` units, and has total cholesterol of `$140$`.
 - What would Joe's cholesterol be if he had exercised `$20$` units instead of `$10$`?

---
## Counterfactual Reasoning: Naïve Approach
- Joe is `$60$` years old, exercised `$10$` units, and has total cholesterol of `$140$`.
 - What would Joe's cholesterol be if he had exercised `$20$` units instead of `$10$`?
 
- Use the estimated causally correct regression equation from observational data, with `$A=60$` and `$E=20$`:

$$
`\begin{align}
c &= 99.99+-0.93e + 0.48a \\
 &= 99.99+-0.93\cdot 20 + 0.48\cdot 60 \\
 &= 110.19
\end{align}`
$$
- This is incorrect, because it ignores what we have learned about Joe by measuring what has already happened to him

- This approach estimates `$E(C|do(E=20, A=60))$`
 - We need to estimate the expected value of Joe's cholesterol if he had exercised at `$20$` units, given the previously observed evidence regarding Joe:
`$$E(C_{E=20}|E=10, A=60, C=C_{E=10}=140)$$`

---
## Causal DAGs as Structural Equations
A causal DAG is a set of structural equations with endogenous and exogenous variables.

.pull-left[

```r
n <- 10000
a <- rnorm(n, mean = 50, sd = 10)
e <- 0.3*a + rnorm(n)
c <- 0.5*a + -1*e + rnorm(n, mean = 100, sd = 5)
```

![](overview_causal_inference_files/figure-html/unnamed-chunk-78-1.png)
]

.pull-right[
$$
`\begin{align}
A &= U_a \\
E &= 0.3 A + U_e \\
C &= 0.48 A + -0.93 E + U_c
\end{align}`
$$

`$U = \{U_a, U_e, U_c\}$` is the set of exogenous variables
- Exogenous variables represent background factors with no explantory mechanism encoded in the model

`$V = \{A, E, C\}$` is the set of endogenous variables

- The values of endogenous variables are defined through functions encoded in the model

Given a set of values for `$U$`, the model functions uniquely define the values of `$V$`.
]
???
ON the left is our known true model. On the right are the  structural equations that we estimated earlier from observational data, but with the intercepts replaced with exogenous variables.

---
## What would Joe's Cholesterol Have Been With E=20?
.pull-left[
**Step 1:** Use inferred equations and prior observations from Joe to determine Joe's background factors, `$U$`

Observed: `$A = 60$`, `$E = 10$`, `$C = 140$`

Substitute and solve:
$$
`\begin{align}
A = 60 &= U_a \\
E = 10 &= 0.3 \cdot 60 + U_e \\
C = 140 &= 0.48 \cdot 60 + -0.93\cdot 10 + U_c \\
\\
U_a &= 60 \\
U_e &= -8 \\
U_c &= 120.5
\end{align}`
$$

]

.pull-right[
**Step 2:** Using inferred equations:

$$
`\begin{align}
A &= U_a \\
E &= 0.3 A + U_e \\
C &= 0.48 A + -0.93 E + U_c
\end{align}`
$$

Replace the function for `$E$` with `$20$`, substitute Joe's values for `$U$` and the remaining `$V$` values to determine the counterfactual

`$$E(C_{E=20}|E=10, A=60, C=C_{E=10}=140)$$`
$$
`\begin{align}
A &= 60 \\
E &= 20 \\
C_{E=20} &= 0.48 \cdot 60 + -0.93\cdot 20 + 120.5 = 130.7
\end{align}`
$$
naïve version had `$C = 110.19$`
]

---
### Why the Difference?
The naïve estimate,

`$$E(C|do(E=20, A=60)) = 110.19$$`

does not reflect the fact the Joe's cholesterol, at `$140$`, is higher than expected for a person of Age 60 with 10 units of exercise:

`$$E(C|do(E=10, A=60)) = 119.49$$`

By using Joe's observed data to estimate `$U$`, then substituting `$E=20$` for the original function `$E = 0.3A+U_e$` the resulting structural equations estimate Joe's counterfactual result:

`$$E(C_{E=20}|E=10, A=60, C=C_{E=10}=140) = 130.7$$`

---
## Counterfactual Reasoning Requires a Causal Model
To compute the background factors `$U$` for an individual we need the structural equations.

An incorrect model and set of equations will give an incorrect counterfactual result

A predictive associational model is not causal, so cannot be used for counterfactual reasoning:

- We should not use it to play what if games, such as what would your risk be if you exercised more?

---
# Use of Counterfactual Reasoning
- Average Causal Effect applies to populations, whereas counterfactual reasoning can answer questions about an individual
- Effect of Treatment on the Treated (ETT): 
`$$ETT = E[Y_1 - Y_0|X = 1]$$`
where `$Y_1$` is outcome when treated, `$Y_2$` is outcome when not treated, and `$X = 1$` means all those treated

- Required for Mediation Analysis: what is the direct effect of a treatment, vs the indirect effect as mediated by other factors?
- Effect of additive interventions
 - What is the expected value of an outcome if we add 5mg to the population's existing dosage?

---
# Conclusion
Causal inference from observational data is difficult, but possible

Causal knowledge is required to reason about interventions--associative predictive or risk models are not enough

Analysis of observational health data requires causal inference

Causal Inference Remains Underutilized and Difficult to Master

- Despite considerable research, textbooks, software packages and tutorials, the area is difficult and confusing to learn--there is no single best introductory textbook

- Schisms in the field, such as between the Causal DAG, [Potential Outcomes](https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/), and other groups (see [Andrew Gelman's blog](https://statmodeling.stat.columbia.edu/)) further add to the confusion.

- Awareness of causal inference among those who could benefit from it's application is still quite low, but that is slowly changing

---
# To Learn More
Non-technical intro
- Pearl J, Mackenzie D. [The book of why: the new science of cause and effect.](http://bayes.cs.ucla.edu/WHY/) Basic Books; 2018 May 15.

Best technical intro

- Pearl J, Glymour M, Jewell NP. [Causal inference in statistics: A primer.](http://bayes.cs.ucla.edu/PRIMER/) John Wiley & Sons; 2016 Mar 7.

Best Practical Intro (including potential outcomes and Causal DAGs)

- Hernán MA, Robins JM (2019). [Causal Inference.](https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/) Boca Raton: Chapman & Hall/CRC, forthcoming.

---
# Thanks
.pull-right[.pull-down[

<a href="mailto:todd.r.johnson@uth.tmc.edu">
<i class="fas  fa-paper-plane "></i> todd.r.johnson@uth.tmc.edu
</a>

<a href="https://github.com/tjohnson250/overview_causal_inference">
<i class="fas  fa-link "></i> https://github.com/tjohnson250/overview_causal_inference
</a>

<a href="http://twitter.com/johnsontoddr4">
<i class="fab  fa-twitter "></i> @johnsontoddr4
</a>

<a href="https://github.com/tjohnson250">
<i class="fab  fa-github "></i> @tjohnson250
</a>

]]

---
exclude: true
### Does Estrogen Replacement Therapy (ERT) Cause Uterine Cancer?
In the 1970's

- ERT widely prescribed to women after menopause
- Several studies found an association between ERT and uterine cancer
- ERT known to cause bleeding in some women
- Uterine cancer can cause bleeding

Two Hypotheses

- ERT causes uterine cancer
- ERT does not cause cancer, but causes bleeding, leading to a uterine exam, which increases the chance of finding undiagnosed uterine cancer

Yale researchers proposed limiting data analysis to women who have bled

Harvard researchers argued that such an analysis could find an association between ERT and Cancer even if ERT did not cause cancer

---
exclude: true
## Causal DAGs for each hypothesis
.pull-left[
![](overview_causal_inference_files/figure-html/unnamed-chunk-80-1.png)
]
---
exclude: true
## Adjust done at data collection or analysis (from Elwert)

---
exclude: true
## Causal DAGs and Joint Probability Distributions
.pull-left[
Any distribution generated by a Markovian causal DAG `$M$`, can be written as:

`$$P(v_1,v_2,...,v_n) = \prod_{i} P(v_{i}|pa_i)$$`

where `$V_1, V_2,..., V_n$` are the variables in `$M$`, and `$pa_i$` are the values of the parents of `$V_i$` in M.
]

.pull-right[
![](overview_causal_inference_files/figure-html/unnamed-chunk-81-1.png)

`$$P(a,e,c)=P(a)*P(e|a)*P(c|a, e)$$`
]

For example, the probability that a patient has A=50, E = 5, and C = 120 is given by:

`$$P(A=50,E=5,C=120)=P(a=50)*P(e=5|a=50)*P(c=120|a=50, e=5)$$`

.whisper[Technical notes: A graph is Markovian if there are no cycles and all error terms jointly indpendent.]
  
---
exclude: true
# Overadjustment Bias

---
exclude: true
## Intervening Changes the Generative Model
.pull-left[
Dichotomous Observational Generative Model

```r
n <- 10000
g <- rbinom(n, 1, .5)
*p_x_g <- c(1/3, 2/3)
*x <- rbinom(n, 1, p_x_g[g]) # Male: 1/3, Female: 2/3 
# gender  treatment p(heart attack)
#  male       0           .3
#  male       1           .4
# female      0           .05
# female      1           .07
p_h_gx = c(.3, .4, .05, .075)
h <- rbinom(n, 1, p_h_gx[g*2+x+1])
```
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-83-1.png" width="100%" />
]
.pull-right[
Dichotomous Interventional Generative Model

```r
n <- 10000
g <- rbinom(n, 1, .5) 
*x <- rbinom(n, 1, .5) # Random chance
#          m¬t  mt  f¬t  ft
p_h_gx = c(.3, .4, .05, .075) # p(H|M,T)
h <- rbinom(n, 1, p_h_gx[g*2+x+1])
```
<img src="overview_causal_inference_files/figure-html/unnamed-chunk-85-1.png" width="100%" />

```r
# CPT of h given g and x
p_h = dint %>% group_by(G, X) %>% summarise(p_h = sum(H == 1)/n())
xtabs(p_h ~ G+X, p_h)
```

```
##    X
## G            0          1
##   0 0.30351438 0.39258669
##   1 0.05252359 0.06901961
```
]

---
exclude: true
# CPT in R
P(h|g,x)

```r
# CPT of h given g and x, with marginals
p_h = dint %>% group_by(G, X) %>% summarise(p_h = sum(H == 1)/n())
addmargins(xtabs(p_h ~ G+X, p_h))
```

```
##      X
## G              0          1        Sum
##   0   0.30351438 0.39258669 0.69610106
##   1   0.05252359 0.06901961 0.12154320
##   Sum 0.35603797 0.46160630 0.81764427
```

---
exclude: true
## GGPlotly graph
<div id="htmlwidget-2d061379d2bd689aae63" style="width:100%;height:504px;" class="widgetframe html-widget"></div>
<script type="application/json" data-for="htmlwidget-2d061379d2bd689aae63">{"x":{"url":"overview_causal_inference_files/figure-html//widgets/widget_unnamed-chunk-88.html","options":{"xdomain":"*","allowfullscreen":false,"lazyload":false}},"evals":[],"jsHooks":[]}</script>